本文共 1442 字，大约阅读时间需要 4 分钟。

题目描述：

给你一棵二叉树，它的根为 root 。请你删除 1 条边，使二叉树分裂成两棵子树，且它们子树和的乘积尽可能大。

由于答案可能会很大，请你将结果对 10^9 + 7 取模后再返回。

示例 1：

输入：root = [1,2,3,4,5,6] 输出：110 解释：删除红色的边，得到 2 棵子树，和分别为 11 和 10 。它们的乘积是 110 （1110）

示例 2：

输入：root = [1,null,2,3,4,null,null,5,6]

输出：90

解释：移除红色的边，得到 2 棵子树，和分别是 15 和 6 。它们的乘积为 90 （156） 示例 3：

输入：root = [2,3,9,10,7,8,6,5,4,11,1]

输出：1025 示例 4：

输入：root = [1,1]

输出：1

提示：

每棵树最多有 50000 个节点，且至少有 2 个节点。

每个节点的值在 [1, 10000] 之间。

来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/maximum-product-of-splitted-binary-tree 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

/** * Definition for a binary tree node. * public class TreeNode { *     int val; *     TreeNode left; *     TreeNode right; *     TreeNode(int x) { val = x; } * } */class Solution {   	long result = 0;	long mod = 1000000000 + 7;	public int maxProduct(TreeNode root) {		if (root == null)			return 0;		get(root);		long sum = root.val;		pre(root, sum);		return (int) (result % (mod));	}	public void pre(TreeNode node,long sum) {		if(node == null){			return ;		}		result = Math.max(((sum - node.val) * node.val) , result);		pre(node.left, sum);		pre(node.right, sum);	}	public int get(TreeNode node) {		if (node == null)			return 0;		int left = get(node.left);		int right = get(node.right);		node.val = (int) (left+ right+ node.val);        		return node.val;	}}

这道题我思路很快就写出来了，其实很简单，但是取模的时候有点粗心

把其实 (int)get % mod 和 (int)（get % mod）是不一样的，以后记住了！！！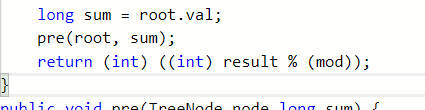

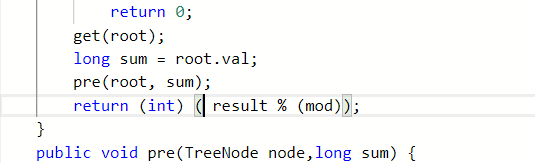
这两种是不一样的！！！，上面的直接转化肯定会出错，我一开始就卡在这里卡了一个多小时哎，不说了都是泪，基础不好啊